Napoleon’s Triangle: A Beautiful Geometric Result 

Napoleon’s Triangle is a fascinating concept in geometry, named after the famous French military leader Napoleon Bonaparte.

Why Is It Called Napoleon’s Triangle?

The connection to Napoleon Bonaparte is somewhat mysterious. There is no concrete historical evidence that Napoleon himself discovered this theorem. However, he was known to have a keen interest in mathematics and geometry. Some historians speculate that Napoleon may have posed or studied the problem, which could have led to its association with his name. Others believe it was simply named after him as a tribute to his reputation for strategic and geometric thinking.

Construction of Napoleon’s Triangle

To construct Napoleon’s Triangle:                          

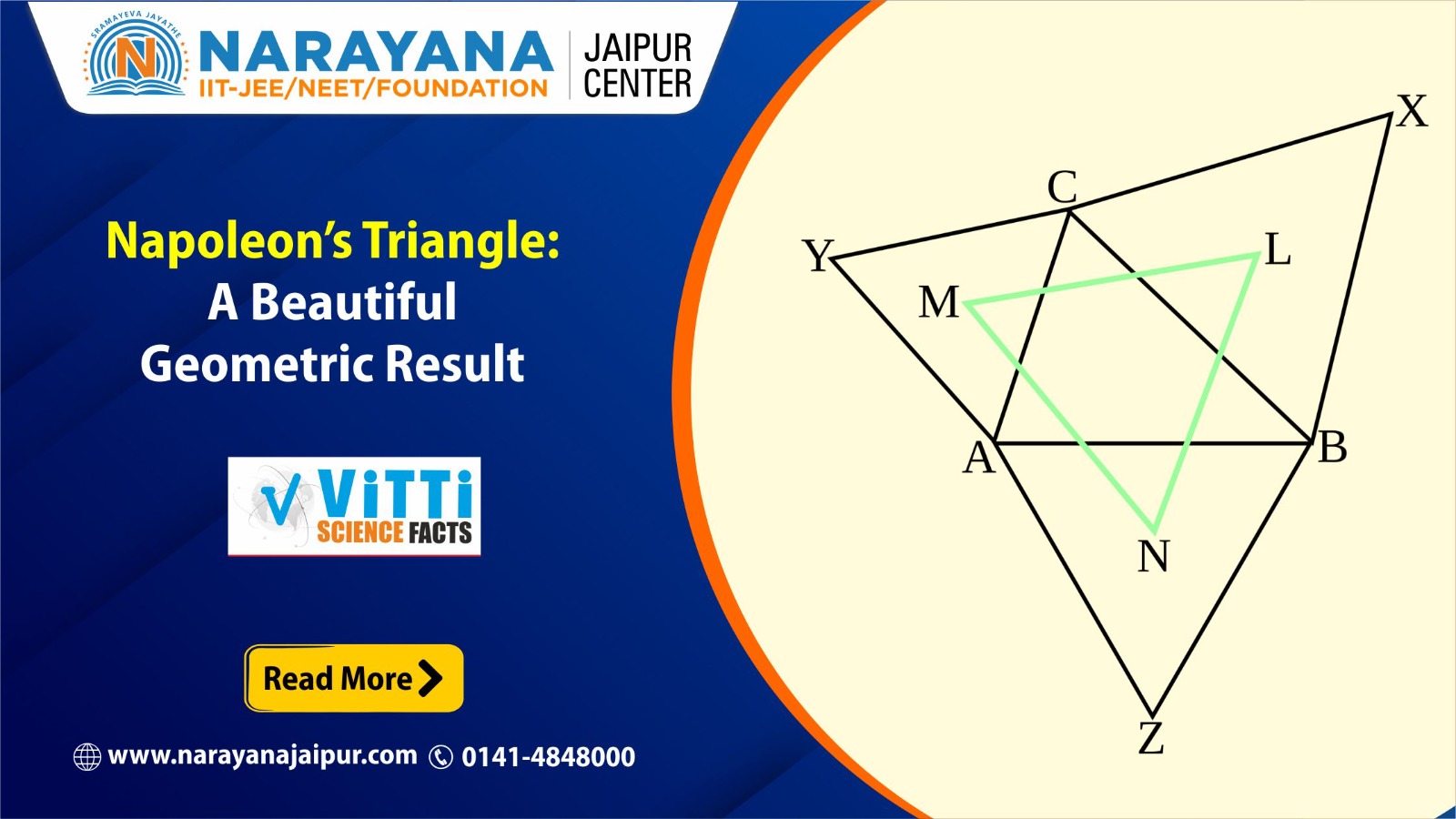
• Start with any given triangle (let’s call it ABC).
• Construct an equilateral triangle on each of its three sides (AB, BC, and CA), oriented outward or inward.
• Locate the centroids (geometric centers) of these three equilateral triangles.
• Connect these centroids to form a new triangle.

This newly formed triangle is called Napoleon’s Triangle, and an incredible property is that it is always equilateral.

Proof of Napoleon’s Theorem

1. Let the vertices of the original triangle be labelled A, B, and C.
2. The centroids of the equilateral triangles formed externally are named as X, Y and Z
3. The rotation Y₁₂₀ maps A to C.  The rotation X₁₂₀ maps C to B.  So if we define S = X₁₂₀Y₁₂₀, then S(A) = X₁₂₀(Y₁₂₀(A)) = X₁₂₀(C) = B. 
4. But by the theory of composition of rotations, S is a rotation by angle 240 degrees and the center D of S is constructed as the vertex of a triangle YXD, where angle X = 120/2 = 60 degrees and angle Y also = 60 degrees.  Thus, YXD is an equilateral triangle.
5. But also, Z₂₄₀(A) = B, since Z₂₄₀ is a symmetry of the triangle ABC’.  This means that we now have two rotations, Z₂₄₀ and D₂₄₀, and in both cases the image of A is B:
6. Z₂₄₀(A) = B
7. D₂₄₀(A) = B
8. But there is only one rotation by 240 degrees that sends A to B.  From this relationship, ABZ and ABD are congruent isosceles triangles, with angle Z = angle D = 120 degrees.  Since the side AB is shared, either Z = D or Z  is the reflection D’ of D in AB.  But the rotation centered at D’ that takes A to B has rotation angle 120, not 240.  Thus Z = D and so XYZ is an equilateral triangle.
9. If the equilateral triangles are drawn inward instead of outward, the centroids will also form an equilateral triangle, proving that both outer and inner Napoleon’s Triangles are equilateral.

Facts about the Fermat Point

In the same figure construct the segments AA’, BB’, CC’.  Also, let C1, C2, C3 be the circumcircles of the 3 equilateral triangles with centers at X, Y, Z.  The following is true:

• All the segments AA’, BB’, CC’ have the same length.
• Any two of these segments meet at an angle of 60 degrees.
• The segments AA’, BB’, CC’ are concurrent at a point F.

All the circles C1, C2, C3 are concurrent at F.

Name: Ashish Khare
Department: Maths, JEE
Narayana Jaipur Center (NIHQ)